Angora

introduction

Angora的关键技术：

Context-sensitive branch coverage：(经验总结)通过将上下文加入branch coverage能使Angora探索到更多的程序状态
可扩展的字节级污点分析：Angora仅变异路径约束依赖的字节位
基于梯度下降的搜索：Angora使用梯度下降算法来解决路径约束，而不是符号执行
Type and shape inference：输入中的许多字节在程序中共同作为单个值。
输入长度探索：只有当输入长度超过一定的阈值时，程序才可以探索到某些状态，但是符号执行和梯度下降都不能告诉fuzzer何时增加输入的长度。Angora检测输入的长度何时会影响路径约束，然后适当的增加输入长度

Background: American Fuzzy Lop(AFL)

AFL是一个现代的基于变异的灰盒fuzzer。AFL使用轻量级的编译时插桩和遗传算法来自动发现可能触发目标程序内部新状态的测试用例。作为基于coverage的fuzzer，AFL生成输入以遍历程序中不同的路径以触发错误。

Branch coverage

AFL通过一组分支来衡量一个路径。在每次运行时，AFL统计每个分支执行的次数。AFL用一个tuple(l~prev~,l~cur~)代表一个分支，两个元素分别为条件语句前后的基本块的ID。AFL使用轻量级插桩来获取分支覆盖度信息。该插桩在编译时注入到每个分支点。对于每次运行，AFL分配一个路径跟踪表，以计数每个条件语句的每个分支各执行了多少次。该表的索引是分支的hash，h(l~prev~,l~cur~)其中h是一个hash函数

AFL同时维护一个跨不同运行的全局分支覆盖度表。每个条目包含一个8位向量，记录分支在不同运行中执行的次数。该向量b中每一位b~0~…b~7~分别代表该分支运行次数位于区间[1],[2],[3],[4,7],[8,15],[16,31],[32,127],[128,+∞)。

AFL比较上述两个表，启发式地确定新输入是否触发了程序的新状态。如果发生以下任一情况，则输入会触发新的状态：

程序执行了一个新分支。路径跟踪表中有一个分支条目，而分支覆盖表中没有这个分支条目
存在一个分支，当前运行中执行的该分支的次数n与之前的运行都不同。AFL通过检查n是否与分支覆盖表的相应位向量对应来大致确定这一点。

Mutation strategies

AFL对输入随机的应用以下变异：

bit或byte翻转
尝试设置”interesting”字节，字或双字
对字节，字或双字增或减一个小整数
完全随机的单字节集合
通过覆写、插入或块memset进行块删除或块复制

Design

Overview

AFL和其他相似的fuzzer使用分支覆盖度作为测度。然而他们在计算分支覆盖度的时候都没有考虑调用上下文，并不能充分探索程序状态。本文提出上下文敏感的分支覆盖度作为覆盖度的测度

Angora的两个阶段：instrumentation和fuzzing loop

// Algorithm 1 Angora’s fuzzing loop. Each while loop has a budget (maximum allowed number of iterations)
function FUZZ(program,seeds)
	Instrument program in two versions: program_nt(no taint tracking) and program_t (with taint tracking).
	branches ← empty hash table ▷ Key: an unexplored branch b. Value: the input that explored b’s sibling branch.
	for all input ∈ seeds do
		path ← Run program_t(input)
		for all unexplored branch b on path do
			branches[b] ← input
		end for
	end for
	while branches is not empty do
		Select b from branches
		while b is still unexplored do
			Mutate branches[b] to get a new input input' (Algorithm 5)
			Run program_nt(input')
			if input' explored new branches then
				path' ← Run programt(input')
				for all unexplored branch b' on path' do
					branches[b'] ← input'
				end for
			end if
			if b was explored then
				branches ← branches − {b}
			end if
		end while
	end while
end function

在fuzzing loop的每次迭代中，Angora会选择一个为探索的分支，并搜索一个会探索该分支的输入。

找到该输入的关键技术：

对于大多数条件语句，其predicate仅受输入中的几个字节的影响，因此没有必要对整个输入进行变异。Angora在探索分支时会确定输入中的哪些字节会流入相应的谓词，并专注于变异这几个字节。
在确定变异哪些输入字节后，Angora需要决定如何变异它们。Angora不使用随机的基于启发式的变异，Angora将分支的路径约束看做对输入上的黑盒函数的约束，并采用梯度下降算法求解约束。
在梯度下降期间，Angora根据参数评估该黑盒函数，其中某些参数由多个字节组成。如果一组连续字节作为一个大整数进入条件语句，则应将这一连续字节作为单个参数而不是独立参数。为了实现此目标，需要推断输入中哪些字节是组合成单个值，以及该值的类型是什么。
某些错误只有在输入长度超过阈值之后才触发。如果输入太短，无法触发错误；如果输入太长，会拖慢程序运行速度。Angora检测何时较长的输入可以探索到新的分支并确定所需的最小长度。

下图展示了模糊测试一个条件语句的步骤。

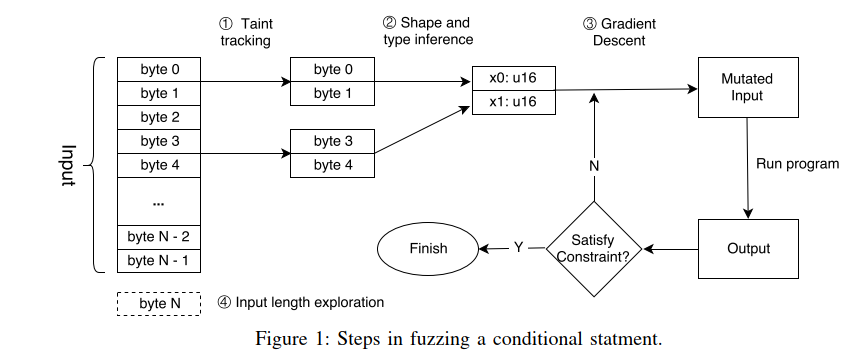
下列代码展示了上述的核心技术

void foo(int i, int j) {
    if (i * i - j * 2 > 0) {
    	// some code
    } else {
    	// some code
    }
}

int main() {
    char buf[1024];
    int i = 0, j = 0;
    if(fread(buf, sizeof(char), 1024, fp) < 1024) {
    	return(1);
    }
    
    if(fread(&i, sizeof(int), 1, fp) < 1){
    	return(1);
    }
    if(fread(&j, sizeof(int), 1, fp) < 1){
    	return(1);
    }
    foo(i, j);
}

字节级污点跟踪：在模糊测试Line 2的条件语句时，Angora使用字节级污点跟踪，确定字节1024-1031会流入此表达式，因此仅对这些字节进行变异。
基于梯度下降的搜索算法：Angora需要找到分别运行在条件语句的两个分支的输入。Angora将条件语句中的表达式视为输入x上的函数f(x)，并使用梯度下降找到两个输入x和x’，使得f(x)>0且f(x')<=0。
Shape and type inference:在梯度下降过程中，Angora分别计算x在x的每个分量上的f的偏导数，所以Angora必须确定每个分量以及它们的类型。在Line 2。Angora确定了x包含两个分量且每个分量包含输入中的4字节，其类型为32位有符号整数。
输入长度探索：除非输入有至少1032字节，否则main不会调用foo。Angora测量从输入中读取并确定较长的输入是否会探索新状态的常见函数，而不是盲目尝试较长的输入。

Context-sensitive branch count

AFL的分支覆盖表的设计有几个优点：

节省空间。分支的数量对于程序的大小是线性关系。
使用范围(range)来计数分支执行能为一个不同的执行是否指示程序的新状态提供良好的启发。当执行计数很小时，计数的任何变化都是很明显的；但当执行计数很大时，只有变化足够大才会被认为是重要的。

但是这个设计也具有局限性。因为AFL的分支是上下文不敏感的，因此无法区分在不同上下文中的相同分支的执行，这可能会忽略新的程序内部状态。下列代码体现了这个问题：

void f(bool x) {
    static bool trigger = false;
    if (x) {
        if (trigger) {
            if (input[2]) {
	            // crash;
            }
        }
    } else {
        if (!trigger) {
            trigger = true;
        }
    }
}

bool[] input;

int main() {
    f(input[0]);
    ...
    f(input[1]);
}

考虑Line 3的分支的覆盖度。在第一次运行的时候，程序输入(10)~b~，当它调用Line 19的f()时，程序执行Line 4的真分支。之后当它调用Line 21的f()时，它执行Line 10的f()。由于AFL对分支的定义是上下文不敏感的，AFL认为两个分支都被执行了。

当程序的输入为(01)~b~时，AFL认为Line 4和Line 10的分支都在上一次运行时执行了，因而这个输入没有触发新的内部状态。但是事实上这个新输入触发了一个新的内部状态，因为当input[2]==1时，程序会在Line 6上触发崩溃。

本文将上下文合并到分支的定义中。本文将分支定义为tuple(l~precv~,l~cur~,context)，前两个元素分别为条件语句前后的基本块的ID，context是h(stack)，h是哈希函数，stack包含调用栈的状态。例如分支(l~3~,l~4~,[l~19~])和分支(l~3~,l~10~,[l~21~])

为分支添加上下文会增加唯一分支的数量，当深度递归发生时，这可能会非常明显。本文当前的实现方式通过使用哈希函数h计算调用栈的哈希值来缓解该问题，其中h计算栈上所有调用站点的ID的异或。当Angora检测程序时，它将为每个调用站点分配一个随机ID。因此，当函数f递归调用自身时，无论Angora将同一个调用站点的ID push到调用栈多少次，h(stack)最多输出两个唯一值，最多会使f函数中唯一分支数增加一倍(个人见解，进入递归的调用站点是一个站点，函数内递归调用是另一个站点)。本文评估表明，在合并上下文后，唯一分支的数量增加了多大7.21倍，以此为代价获得了改进的代码覆盖度。

Byte-level taint tracking

Angora的目标是生成能执行未探索分支的输入。Angora需要字节级污点跟踪，以此确定输入的哪些字节会影响分支的predicate。但是AFL不使用污点跟踪，因为它开销太大，特别是在分别跟踪每个字节时。本文对此的一个关键的观点是：污点跟踪在程序的大多数运行中都是没有必要的。即在使用污点跟踪观察记录到输入的哪些字节会流入条件语句之后，在之后的运行中就变异这些字节而不再需要运行污点跟踪。Angora以此策略实现了与AFL相仿的吞吐量(throughput)。

Angora将程序中的每个变量与污点标签t~x~相关联，该污点标签表示可能流入x的输入中的字节偏移。污点标签的数据结构对其内存占用量有很大影响。一个naive的实现方式是将每个污点标签表示为一个位向量，其中每个位i代表输入的第i个字节。但是这种实现下这个位向量的大小会随着输入的大小线性增长，因而此数据结构无法应用于大输入，但是在程序中挖掘漏洞，大输入是必要的。

本文将位向量存储在一张表中，用索引作为污点标签，以此减少污点标签的大小。只要表中条目数的对数远小于最长位向量的长度（通常是这种情况），就可以显著减小污点标签的大小。

但是，此数据结构又提出了新的挑战。污点标签必须支持下列操作：

INSERT(b)：插入一个位向量b并返回它的标签
FIND(t)：返回污点标签t指向的位向量
UNION(t~x~,t~y~)：返回代表污点标签t~x~和t~y~指向的位向量的联合的污点标签

FIND开销小，但是UNION开销很大。UNION需要经过以下步骤：

它找到两个标签的位向量并计算它们的联合u，这个步骤开销小
它搜索整个表来确定是否u已经存在。如果没有，则加入u。问题在于如何搜索。线性的搜索开销极大。取而代之的，可以建立一个位向量的哈希集合，但是如果存在大量的位向量，而每个位向量都很长，那么将需要花费极大的时间来计算哈希值，以及需要大量空间来存储哈希集合。UNION是一个污点跟踪算术表达式中数据的常用操作，因此它必须高效。注意不能使用UNION-FIND数据结构，因为这些向量不是不相交的。

本文提出一个新的数据结构用于存储位向量，并实现了高效的INSERT，FIND和UNION。对于每个位向量，数据结构使用一个无符号整数为其分配一个唯一的标签。当程序插入一个新的位向量时，数据结构为其分配下一个可用的无符号整数。

数据结构包含两个部分：

一个二叉树，将位向量与他们的标签作映射。每个位向量b被一个唯一的深度为

的树节点v~b~代表，

为位向量b的长度。 v~b~存储b的标签。从根到达v~b~将依次检索b~0~，b~1~……。如果b~i~是0，搜索左子树，否则，搜索右子树。每个节点包含一个指向其父节点的后向指针，使得我们能够从节点v~b~检索位向量。

查找表将标签映射到它们的位向量。标签是此表的索引，并且相应的条目指向代表该标签的位向量的树节点。

在这个数据结构中，树中所有的叶节点都代表位向量，并且没有内部的节点代表叶节点。然而树中的许多节点可能没有必要。例如(本示例用正则表达式通用符号，其中x*表示x重复零次或多次，[xy]表示x或y)，如果树中有一个向量x00*，但是树中没有向量x0[01]*1[01]*，其中x表示任意的位序列，那么就不必在该节点之后存储代表x的节点(这个看起来不是树结构上的先后问题，这个after指的应该是时间上的先后，即存储该节点，然后存储x节点这个”先后”)，因为x只有一个后代是叶节点，而这个叶节点代表x00*。这个思路可以指导我们在将向量插入树中时可以修剪向量：

删除向量所有的末尾的0
从第一位到最后一位跟随向量中的位遍历树
- 如果某位是0，则跟随左子节点
- 否则，跟随右子节点
- 如果缺少子节点，创建它
将向量的标签存储在访问的最后一个节点中

INSERT操作的算法

function INSERT(root, vector, nodes) 
//root: root of the tree. vector: the vector to be inserted.
//nodes: an array indexed by labels containing pointers to tree nodes. 
//return: the label representing vector.
	Trims all the trailing 0s in vector
	if vector is empty then
		if root contains no label then
			root.label ← nodes.length() // Assigns the next available integer as the label for this vector.
			nodes.push(root)
		end if
		return root.label
	end if
	if vector[0] == 0 then
		node ← root.left
	else
		node ← root.right
	end if
	if node does not exist then
		Creates node
		if |vector| == 1 then
			node.label = nodes.length() //Assigns the next available integer as the label for this vector.
    		nodes.push(node)
    	end if
	end if
	if |vector| == 1 then
		return node.label
	else
		return INSERT(node, vector[1..], nodes) //vector[1..] is vector after first element removed.
	end if
end function

FIND操作的算法：

function FIND(label, nodes)
//label: an integer representing a tree node, which represents a bit vector. 
//nodes: an array indexed by labels and containing pointers to tree nodes. 
//return: the bit vector represented by label.
	vector ← empty vector
	node ← nodes[label]
	parent ← node.parent
	while parent exists do
		if node is the left child of parent then
			vector.insert at beginning(0)
		else
			vector.insert at beginning(1)
		end if
			node ← parent
			parent ← node.parent
	end while
	return vector
end function

UNION操作的算法：

function UNION(label1, label2, nodes, root) 
//label1, label labels of two bit vectors.
//nodes: a table containing pointers to tree nodes.
//root: root of the tree.
//Return: the label representing the union of the bitvectors.
	v1 ← FIND(label1, nodes)
	v2 ← FIND(label2, nodes)
	v ← v1 ∪ v2
	return INSERT(root, v, nodes)
end function

注意，当我们创建节点时，该节点初始化时是没有标签的。然后，如果这个节点是我们插入一个位向量时访问的最后一个节点，我们就将这个位向量的标签存储在这个节点中。通过这个优化，该二叉树具有以下特性：

每个叶节点都包含一个标签
一个内部节点可能包含一个标签。我们可能会将标签存储在还没有标签的内部节点中，但是我们永远不会替换任何内部节点的标签。

该数据结构大幅减少了用于存储位向量的内存占用。设每个位向量长度为n，有l个位向量。如果将所有的位向量存储在表中，则将占用O(nl)空间。而上述数据结构，树中的节点数为O(l)。每个节点最多可以存储一个查找表索引。由于查找表具有l个条目，并且每个条目都是一个指针，因此具有固定的大小，因此查找表的大小为O(l)，并且查找表的每个索引都具有O(log(l))位。因此，该数据结构所需总空间为O(l*log(l))

Search algorithm based on gradient descent

字节级别的污点跟踪确定了输入的哪些字节偏移会流入条件语句。接下来就是解决如何变异这些输入以探索到语句的未探索分支的问题。大多数Fuzzer随机或者使用粗糙的启发式算法进行变异，但是这种做法似乎并不能很快的找到合适的输入。Angora将其视为一个搜索问题，并且使用机器学习中的搜索算法解决问题。Angora在此选择梯度下降算法(此处的原文称”We used gradient descent in our implementation, but other search algorithms might also work.”，此处是否暗示作者仅用一些理论甚至随意的选择了梯度下降，而并没有考虑其他的算法)

在这种方法中，Angora将执行分支的predicate视为对黑盒函数f(x)的约束，其中x是流入predicate的输入值的向量，f(x)捕获对从程序的开始到这个predicate的路径的计算。f(x)上有三类约束：

f(x)<0
f(x)<=0
f(x)==0

即可以将所有形式的比较转换成上述三个约束：

Comparison	f	Constraint
a<b	f=a-b	f<0
a<=b	f=a-b	f<=0
a>b	f=b-a	f<0
a>=b	f=b-a	f<=0
a==b	f=abs(a-b)	f==0
a!=b	f=-abs(a-b)	f<0

如果条件语句的predicate中包含逻辑操作符&&或||，Angora将其分割为多个条件语句。例如：

if(a&&b)
	{s}
else
	{t}

Angora会将其分割为：

if(a)
{
    if(b)
        {s}
    else
    	{t}
}
else
	{t}

搜索算法如下：

function FUZZCONDITIONALSTMT(stmt, input)
//stmt: The conditional statement to fuzz. 
//input: The input to the program
	repeat
		grad ←CALCULATEGRADIENT(stmt, input)
		if grad == 0 then
			input ← RESAMPLE(input)
			Continue to the next iteration
		end if
		input, value ← DESCEND(stmt, input, grad)
	until SATISFYCONSTRAINT(stmt, value) or timeout
end function

算法从x~0~开始，找到使f(x)满足约束的x。为了满足每种约束条件，我们需要最小化f(x)，出于这个目的，Angora使用梯度下降。

梯度下降寻找f(x)的最小值。该方法是迭代的。每次迭代都从x开始，计算$\nabla _x f(x)$，并将x的值更新为$x-\alpha \nabla _x f(x)$，此处$\alpha$为学习率。

在训练神经网络时，研究人员使用梯度下降来找到一组权重，以最小化训练误差。但是，梯度下降存在局部最优解不是全局最优解的问题。但是这对于模糊测试来说通常不是问题，因为模糊测试中并不需要全局最优解，只需要找到一个足够好的输入x即可。例如，对于约束f(x)<0，只要找到一个x是的f(x)<0即可，而不需要找到f(x)的最小值。

但是将梯度下降应用于模糊测试时面临着独特的挑战。梯度下降需要计算梯度$\nabla _x f(x)$。在神经网络中，可以用解析形式(analytic form)写$\nabla _x f(x)$，但是在模糊测试中没有f(x)的解析形式。其次，在神经网络中f(x)是一个连续函数，因为x包含网络的权重，但是模糊测试中f(x)通常是一个离散函数。这是因为典型程序中的大多数变量都是离散的，因此x中的大多数元素都是离散的。

Angora使用数值逼近法(numerical approximation)解决了这些问题。f(x)的梯度是唯一的向量场，其在每个点x与任何单位向量v的点积是f沿着v的方向导数。Angora将每个方向导数近似为$\frac{\partial f(x)}{\partial x_i} = \frac{f(x+\delta v_i)-f(x)}{\delta}$，其中$\delta$是一个小的正数(比如1)并且$v_i$是第i维的单位向量。为了计算每个方向导数，Angora需要运行两次程序，一次使用原始输入$x$，第二次使用扰动的输入$x +\delta v_i$。在第二次运行中，程序可能无法到达计算$f(x +\delta v_i)$的程序点，因为程序在较早的条件语句中采用了另一个分支。发生这种情况时，Angora将δ设置为较小的负数（例如-1），然后尝试再次计算$f(x +\delta v_i) $。如果成功，Angora将基于此计算方向导数。否则，将导数设置为零，指示梯度下降不要沿该方向移动$x$。由于Angora会分别计算每个方向导数，因此计算梯度的时间与向量$x$的长度成正比。

Shape and type inference

如果只是很简单的将$x$中的每个元素成为流入predicate的一个字节，会导致类型不匹配，从而使得梯度下降出问题。例如将输入的四个连续字节b~3~b~2~b~1~b~0~视为一个整数，并用x~i~表示此整数值。在计算$f(x +\delta v_i) $时，应当将$\delta$加到整个整数上。但如果将每个字节分配给x中的不同元素，那么将会在每个字节上计算$f(x +\delta v_i) $，显然这是不合适的。

为了避免这个问题，就必须确定：

输入中的哪些字节始终在程序中组合成为单个值发挥作用
这个值的类型是什么

Angora将第一个问题称为Shape inference，第二个问题称为Type inference，并在动态污点分析过程中加以解决。

对Shape inference，初始化输入时所有字节都是独立的。在污点分析期间，当指令读取了一个输入字节序列进入变量，而序列的size与原类型(primitive type)的size相匹配时(例如1、2、4、8字节)，Angora会将这些字节标记为属于同一个值。当发生冲突时，Angora使用最小的size。

对Type inference，Angora依赖于对值进行操作的指令的语义。例如，如果指令对有符号整数进行运算，则Angora会将相应的操作数推断为有符号整数。当相同的值同时用作有符号和无符号类型时，Angora会将其视为无符号类型。

当Angora无法推断出值的精确大小和类型时，这不会阻止梯度下降找到一个解-只是需要花费更长的时间。

Input length exploration

与其他大多数fuzzer类似，Angora在fuzz时会从尽可能小的输入开始。但是只有当输入长度超过某个阈值时，一些分支才会被执行。这使fuzzer陷入了两难困境。如果fuzzer使用的输入太短，则无法探索这些分支；但如果使用的输入太长，则可能会拖慢运行速度，甚至内存耗尽。大多数工具使用将就的(ad hoc)方法尝试不同长度的输入。相比之下，Angora仅在有可能探索到新分支时才增加输入长度。

ad hoc testing:除非发现缺陷，否则测试仅打算运行一次。临时测试是最不正式的测试方法。

在污点跟踪期间，Angora将read-like函数调用中的目标内存与输入中的相应字节偏移量相关联。并使用特殊标签标记read的返回值。如果在条件语句中使用了这个返回值且不满足约束条件，则Angora会增加输入长度，以便read可以获得其请求的所有字节。

例：

void foo(int i, int j) {
    if (i * i - j * > 0) {
    	// some code
    } else {
    	// some code
    }
}

int main() {
    char buf[1024];
    int i = 0, j = 0;
    if(fread(buf, sizeof(char), 1024, fp) < 1024) {
    	return(1);
    }
    if(fread(&i, sizeof(int), 1, fp) < 1){
    	return(1);
    }
    if(fread(&j, sizeof(int), 1, fp) < 1){
    	return(1);
    }
    foo(i, j);
}

如果第12行的条件语句为False，则Angora会扩展输入长度，以便fread可以读取其请求的所有1024个字节。

但是该标准不是详尽的，因为程序可能会使用Angora意料之外的方式来使用(consume)输入并检查其长度。但是只要一经发现，就可以很容易的将其添加到Angora中。

Implementation

Instrumentation

对于要fuzz的每个程序，Angora通过使用LLVM Pass对该程序进行插桩来生成相应的可执行文件。

插桩：

收集条件语句的基本信息，并通过污点分析将条件语句链接到其相应的输入字节偏移量。在每个输入上，Angora仅运行一次此步骤（在变异此输入期间不运行）。
记录执行跟踪以识别新输入。
在运行时支持上下文。
在predicate中收集表达式值。

为了支持可扩展字节级污点跟踪，Angora通过扩展DataFlowSanitizer(DFSan)实现了污点跟踪。并为FIND和UNION操作实现了缓存功能，从而显著加快了污点跟踪。

Angora依赖于LLVM 4.0.0（包括DFSan）。它的LLVM Pass具有820行C++代码（不包括DFSan），运行时具有1950行C++代码，包括用于存储污点标签的数据结构以及用于污染输入和跟踪条件语句的钩子。

除了具有两个分支的if语句外，LLVM IR还支持switch语句，后者可能会引入多个分支。Angora为方便起见，将每个switch语句统一转换为一系列if语句。

当字符串和数组出现在条件语句中时，Angora会识别用于比较字符串和数组的libc函数。例如，Angora将 strcmp(x,y)转换为x strcmp y，其中strcmp是Angora理解的特殊比较运算符。

Fuzzer

本文用4488行Rust代码中实现了Angora。并使用fork服务器和CPU绑定等技术优化了Angora。

组会讨论和问题记录

这篇paper的evaluation中的其他fuzzer的对照数据，看起来是直接从相应的论文中获取的数据。
fuzz是否可以测试其他语言的程序
- 对于依赖于源码的fuzz，这些fuzz需要在编译可执行文件时进行插桩等操作，所以会受限于语言要求；对于仅依赖于binary的fuzz，可能就不受限于语言的限制
fuzz对于hotpatch技术的支持
- 暂时回答不上

组会纪要

2020-02-21 组会纪要